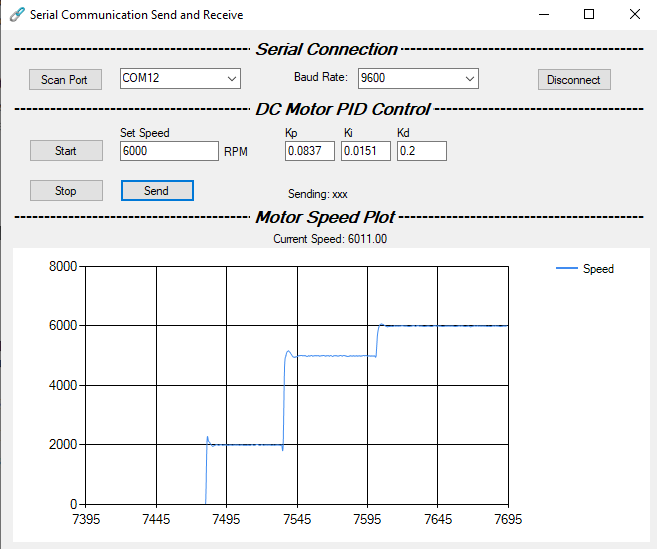
Brushed DC Motor Speed Control_PID
Quick Menu At first, we sample $f(x)$ in the $N$ ($N$ is odd) equidistant points around $x^*$:[ f_k = f(x_k),: x_k = x^*+kh,: k=-frac{N-1}{2},dots,frac{N-1}{2}]where $h$ is some step.Then we interpolate points ${(x_k,f_k)}$ by polynomial begin{equation} label{eq:poly} P_{N-1}(x)=sum_{j=0}^{N-1}{a_jx^j}end{equation}Its coefficients ${a_j}$ are found as a solution of system of linear equations:begin{equation} label{eq:sys} left{ P_{N-1}(x_k) = f_kright},quad k=-frac{N-1}{2},dots,frac{N-1}{2}end{equation}Here are references to existing equations: (ref{eq:poly}), (ref{eq:sys}).Here is reference to non-existing equation (ref{eq:unknown}).